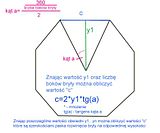
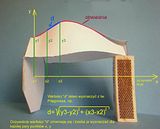
Hmm... Stachu napisał, że
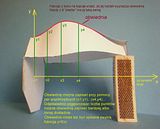
każdy z odcinków "d" leży na symetralnej paska, natomiast tu jego długość jest wyznaczana tak, jakby leżał on na obwiedni. Z pewnością taka metoda nie da dobrego wyniku - zaprojektowany element okaże się za długi.
Nie będzie za długi, bo obwiednia leci właśnie przez symetralną paska.
Zaś Stillman, że
jest to rzeczywista krawędź między tymi fragmentami obu segmentów czyli wyliczenie będzie prawidłowe.
Właśnie wtedy będzie nieprawidłowe.
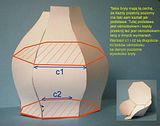
Rzeczywiście odcinki „d” leżą na osi symetrii rozwijanego paska.
Muszą leżeć na tej osi. Oczywiście moim błędem jest niezbyt dokładne wyjaśnienie czym jest ta obwiednia a zdjęcie rzeczywiście sugeruje, że obwiednia leci po zewnętrznej krawędzi paska (miejscu klejenia). A tak nie jest.
Może na tych zdjęciach będzie to widać lepiej.

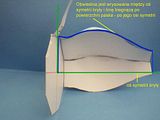

Stach napisał też, że
"Problemem może być także to, że aby zaprojektować element, trzeba mieć już gotową kopułę w 3D - a jak to zrobić mając tylko jej przekrój i liczbę "ścian"?
Tego fragmentu za bardzo nie rozumiem

. Przekrój przecież wystarczy.
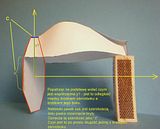
Mój algorytm opiera się wyłącznie na tym przekroju, czy też obwiedni. Wystarczy znać obwiednię i liczbę ścian i można taką bryłę rozwinąć. Oczywiście obwiednia może być w programie wstępnie zadana – jak to jest w Siatkach - jako okrąg, czy elipsa. Ale można też ją opisać przy pomocy par punktów x,y albo wręcz użyć jakiejś funkcji f(x), która ten kształt wykreśli. Zatem wystarczy sobie narysować obwiednię na papierze milimetrowym i odczytać wartości „y’ przy określonym skoku wartości „x”, np. co 0,5 mm.
Oto przykłady takich brył zrobionych przy użyciu arkusza kalkulacyjnego Excel.

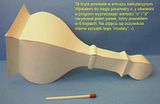
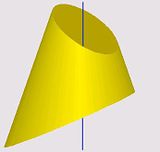
Jeśli chodzi o rozwijanie stożka ściętego pod dowolnym kątem, to przyznam, że nie jest to dla mnie zadanie banalnie proste. Dlatego z chęcią przeczytam opis takiego algorytmu

.
Dla jasności - chodzi mi o taki stożek jak ten na rysunkach z programu Siatki (stożek w 3D i jego rozwinięcie).