JAK SOBIE STOŻEK ŚCIĄĆ I ROZWINĄĆ JEGO POWIERZCHNIĘ:
O tak stożek, jak po lewej:

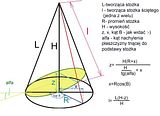
1. Tak wygląda "normalny" stożek od boku.

2. Ścinamy go płaszczyzną pod kątem alfa.

3. Pod stożkiem dorysowujemy rzut jego podstawy, podzielony na ileś identycznych części (tutaj 8).

4. Łączymy oba rzuty odpowiednimi odcinkami. Z wierzchołka rysujemy odpowiednią ilość tworzących.

5. Rysujemy rozwinięcie ściany bocznej "normalnego" stożka. Długość promienia tego wycinka koła to oczywiście długość tworzącej stożka. beta=(D/L)*180st

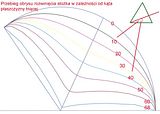
6. Dzielimy rowinięcie na taką ilość części, jak podstawę w pkt. 3.

7. Rysujemy mnóstwo punktów. Odległości między wierzochłkiem stożka i punktami z primami, są takie same, jak odległości między punktem s, a punktami z bisami (ups, zamiast 9" powinno być 1").

8. Łączymy odpowiednie punkty krzywą.

9. I mamy gotowy element.

10. Od dołu zamyka się go oczywiście kołem o odpowiedniej średnicy, a od góry o tym (trochę skomplikowane te rysunki, ale mam nadzieję, że idzie się domyślić, jak to się robi):


Syzyf pisze:Teraz też zastanawiam się, czy podstawa musi być wielokątem foremnym.
Na zdjęciu, które wstawiłem kopuła w niższej partii kościoła ma taki kształt. Jest to ośmiobok, ale na przemian jedna ściana jest szeroka a druga wąska
Da się zrobić, tylko trzeba brać inne alfy (u mnie na 4. rysunku).