Algorytm rozwijania toroidu i stożka ściętego- opis*

[Scooby]

Na prośbę Syzyfa przeniosłem kilka ostatnich postów do nowego wątku Kreski.NET - nowy program do rozwijania

[Syzyf]

Dzięki
Wydaje mi się, że tak będzie bardziej przejrzyście. Tutaj może uda się jeszcze pociągnąć teoretyczno-praktyczne tematy rozwijania brył,a w temacie dotyczącym samych Kresek będzie można wpisywać uwagi i sugestie dotyczące programu w miarę jego rozwoju:

[Syzyf]

Było już trochę o algorytmach, jednak brakuje w tym wątku ich praktycznego wykorzystania. W jaki sposób - w oparciu o dany algorytm i wzory matematyczne - komputer potrafi rozpłaszczyć stożek czy ostrosłup, znając jedynie jego podstawowe wymiary.
Postaram się to wyjaśnić, czyli opisać jak może działać taki program jak Siatki czy Kreski. Będzie to opis uproszczony, ale mam nadzieję zrozumiały przez to dla każdego.

Jak komputer widzi rysunek
Każdy w szkole spotkał się z układem współrzędnych XY. Na takim układzie można łatwo zaznaczyć kropką punkt P, znając jego współrzędne x i y. Jednak w takim układzie liczby x i y mogą być dodatnie albo ujemne oraz mieć wartości ułamkowe, np. x=3,26 a y=-5,67.
Dla przypomnienia


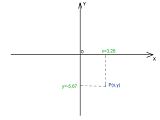
Programy posługują się podobną zasadą, z tym że współrzędne mogą przybierać jedynie wartości całkowite i dodatnie. Operują więc tylko na jednej ćwiartce tego układu, gdzie x i y są dodatnie.
Ćwiartka taka ma również takie ograniczenie, że nie jest nieskończenie wielka - programista musi określić z góry jej wymiary.


Wymiary te muszą być liczbami całkowitymi a "jednostką długości" jest tzw. piksel. Jaka jest długość piksela? Nie ma jej z góry narzuconej. Pisząc program sami decydujemy, jakie są jego wymiary. Na przykład ustalamy sobie, że 1 piksel będzie miał "długość" 0,1 mm. Jeśli więc na rysunku ustawimy obok siebie 100 pikseli, to będzie to odcinek o długości 10 mm. "Rysunek" dla komputera jest więc tabelką o wyznaczonej z góry liczbie kolumn i wierszy, gdzie jedna komórka to piksel.


Jak komputer rysuje i dlaczego trzeba znać aż dwa polecenia
Rysowanie odbywa się w bardzo prosty sposób: podajemy programowi współrzędne piksela i każemy mu przybrać jakiś kolor (pikselowi). Dla uproszczenia przyjmijmy, że na wstępie cały obszar przeznaczony na rysunek ma piksele białe a rysowanie następuje poprzez zmianę koloru piksela na kolor czarny. To dość trudne, bo do poprawnego działania takiego programu trzeba znać aż 2 polecenia!
Brzmią one tak:
1. „Zaczernij piksel o współrzędnych x, y” - nazwijmy je roboczo Punkt(x,y). Wydanie polecenia Punkt(23, 67) zaczerni piksel o takich współrzędnych
2. „Narysuj linię do piksela x, y” - LiniaDo(x,y). Początkiem jest ostatni zaczerniony piksel albo koniec ostatniej linii.

Działanie programu przypomina sterowanie ręką trzymającą ołówek, poruszającą się nad kartką papieru: przesuń się tu czy tam i dziabnij ołówkiem w punkt. Albo: dziabnij, przyciśnij i rysuj do innego miejsca.

I to jest cała potrzebna wiedza do tego, żeby rysować po wyznaczonym obszarze.
Pierwszy program
Oto przykładowy program w roboczym języku i jego wykonanie (komendy wykonywane są po kolei)


Zatem chcąc np. narysować prostą choinkę, należy znać współrzędne potrzebnych punktów i pisać program z głową:


Program pisany bez głowy, podczas tłumaczeniu dziecku skąd się biorą dzieci itp. da taki efekt:


W rzeczywistości istnieje wiele poleceń ułatwiających życie programiście, rysujących od razu gotowe prostokąty czy kółka, ale o tych wyrafinowanych narzędziach nie będę pisał.

Podsumowując: aby narysować cokolwiek należy znać współrzędne pikseli i z sensem je zaczernić. Kluczową sprawą jest więc sposób wyznaczania współrzędnych punktów oraz kolejności wykonywania połączeń między nimi.
A do tego trzeba mieć łeb .

Rozwijamy pierwszą bryłę
Pora więc na pierwszą bryłę: program ma narysować rozwinięcie walca o średnicy 32 mm i wysokości 54 mm.
Rozwinięcie walca jest prostokątem: jeden wymiar to wysokość a drugi to obwód podstawy:
-wysokość= 54 mm
-obwód=PI*32mm=100,48 mm
Zadanie to sprowadza się więc do narysowania prostokąta.
Program przelicza te wymiary na pikselową długość (1 piksel=0,1 mm). Daje to wymiary 1005x540 pikseli. Jak widać dokładność rysowania zależy od ustalonej liczby pikseli na 1 mm. Im więcej, tym rysunek bardziej dokładny.
Program jest zatem dziecinnie prosty:


Gotowy element drukujemy i sklejamy nie zapominając pochwalić się swoim dokonaniem na Forum:


W następnym odcinku spróbuję opisać rozwijanie siatki graniastosłupa foremnego o 5 bokach. Albo więcej
Plus obie podstawy rzecz jasna
Wszelkie uwagi, w tym również o wypisywaniu herezji - wskazane .

A teraz zapraszam na wybory...

[angus]

Programy posługują się podobną zasadą, z tym że współrzędne mogą przybierać jedynie wartości całkowite i dodatnie. Operują więc tylko na jednej ćwiartce tego układu, gdzie x i y są dodatnie.

Trzeba jeszcze pamiętać o tym, że standardowo, w Windowsie, układ współrzędnych jest lekko "przekręcony", tzn. początek układu współrzędnych jest w lewym górnym rogu ekranu (obszaru) a nie lewym dolnym Ale dla chcącego nic trudnego i można to zmienić wykonując proste przekształcenia.

A teraz zapraszam na wybory...

Do dzieła

[Syzyf]

Wybory wygrane
Nic dziwnego, w końcu byłem głosować

Cieszę się, że temat jest też pod czujnym okiem autora Kresek

początek układu współrzędnych jest w lewym górnym rogu ekranu (obszaru) a nie lewym dolnym

To niestety jest prawda, jednak nie chciałem zmieniać przyzwyczajenia czytelników do tego, że wartości Y rosną do góry . Zwróćmy jednak uwagę, że w niczym to nie przeszkadza. Nawet gdybyśmy o tym nie wiedzieli, to program narysuje po prostu rysunek "do góry nogami". Po wydruku wystarczy obrócić kartkę o 180 stopni .
Tak więc zostajemy przy igrekach klasycznych, co by nie mącić. Przynajmniej nie za wiele

Doszedłem do wniosku, że przed opisem rozwinięcia graniastosłupa trzeba jeszcze liznąć nieco teorii. Będą to proste rzeczy, ale niezbędne do zrozumienia dalszych etapów.

Wrócę więc jeszcze do programu rozwijania walca. Podany poprzednio przykład ma ten feler, że rozwija tylko jeden walec o konkretnych wymiarach. Może niektórzy chcieliby rozwinąć swój własny
Program musi więc być uniwersalny i umożliwić zrobienie tego dla różnych wysokości i średnic.
Zmodyfikujemy go tak, aby był w stanie rozwinąć wszystko .

Użytkownik wprowadza do programu dane o wysokości i średnicy. Ponieważ nie wiemy jakie to będą liczby, muszą one zostać zapamiętane. Jak program je zapamiętuje?
Służą do tego celu odpowiednie miejsca w pamięci zwane zmiennymi.
Tutaj garść naprawdę łatwej do ogarnięcia teorii, raptem jeden ekran :

Wiemy już, co to są zmienne czas je zastosować .
Użytkownik wprowadził swoje dane (pal licho jak) i program zapamiętał je w zmiennych: Wysokosc oraz Srednica (gdzieś tam się pałętają po pamięci).
Przeliczmy je na piksele. Ponieważ rozdzielczość wynosi 1 piksel na 0,1 mm zapamiętamy ją też jako zmienną:
Rozdz:=0,1
Zmienne "spikselowane" oznaczymy jako WysP oraz SzerP , co by nie pisać zbyt długaśnych nazw (od razu obliczymy obwód walca, przyjmując że program zna wielkość "Pi"):
WysP:=Wysokosc/Rozdz
SzerP:=Pi*Srednica/Rozdz

Ważną rzeczą w programie są komentarze, które są ignorowane przez komputer ale programiście ułatwiają zapamiętanie co dany fragment robi. Przed komentarzem stawiamy znak //.
Ustalamy, że rysowanie zaczniemy tym razem od punktu w lewym dolnym rogu obszaru rysunku.
Oto wartości początkowe:
Xp:=50 // Xp - współrzędna x początkowa
Yp:=50 // Yp - współrzędna y początkowa

Ustaliliśmy "na stałe" wartości trzech zmiennych: Rozdz, Xp, Yp. Ma to ogromną zaletę: jeśli zajdzie potrzeba zmiany rozdzielczości albo punktu początkowego, to wystarczy to zmienić tylko w tym miejscu programu. Cała reszta będzie operowała na zmiennych wyrażonych przez nazwę. Można pozwolić też użytkownikowi na ustalenie swoich wartości w opcjach programu.
Do narysowania uniwersalnego prostokąta potrzebujemy jedynie znajomości 4 punktów. Oto one:


A oto nasz cały uniwersalny program, który narysuje rozwinięcie każdego walca (tym razem już bez numeracji linii):


Mam nadzieję, że nie bolało. Na dzisiaj wystarczy, bo co za dużo...
W następnym odcinku jeszcze się trochę zapętlę, ale potem już granistosłup, na który wszyscy czekają .

[Syzyf]

Dzisiaj będzie kilka słów o pętlach.
Nie chodzi tutaj o sposób, jak zgrabnie i szybko zawiązać pętlę by powiesić się, gdy program nie działa.
Garść teorii nie przekracza jak zwykle objętości jednego ekranu - po przeczytaniu kilku, może rzeczywiście trzeba by rozejrzeć się za sznurkiem


Uzbrojeni w pętlę możemy przystąpić do jej wykorzystania.
Napiszmy program, który wykona rysunek podobny to testowego z nowej wersji programu Kreski.NET:

U mnie będzie to jedna pozioma linia o długości 100 mm (1000 pikseli) a na niej 11 pionowych kresek o długości 20 mm (200 pikseli) w odstępach co 10 mm(100 pikseli).
Rysunek pomocniczy:


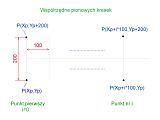
Oraz gotowy program


Jako sprawdzenie nabytej wiedzy proponuję przeanalizować, co narysuje następujący program

Xp:=50
Yp:=50
Powtorz od i:=0 do 10
{
Punkt(Xp+i*30, Yp)
LiniaDo(Xp+70+i*30,Yp+200)
LiniaDo(Xp+140+i*30,Yp)
}
Odpowiedź w kolejnym odcinku, czy ok. niedzieli.
Nie samym programowaniem człowiek żyje.
Czasami trzeba też coś skleić

[Syzyf]

Nic nie skleiłem ale chociaż napisałem kolejny odcinek

Poprawną odpowiedź na pytanie zadane ostatnio wyrysuje komputer, a dokładniej arkusz Excel'a.
Jak widać są to odwrócone literki V, przesuwane w pętli co 30 pikseli:


Rozkładamy graniastosłup foremny, czyli o takiej samej szerokości ścian bocznych.
Ściany Boczne
Wielkości niezbędne do wykonania rozwinięcia takiej bryły są trzy: wysokość, szerokość ściany bocznej oraz liczba boków:


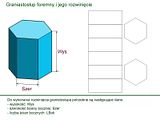
Zacznijmy od prostszego, czyli rozwinięcia ścian bocznych. Składa się ono z szeregu prostokątów o wymiarach zależnych od wysokości i szerokości ściany.
Można jednak nie rysować całych prostokątów, lecz fragmenty w kształcie litery C:


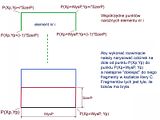
Oczywiście do narysowania tych powtarzających się fragmentów wykorzystamy w programie pętlę. Liczba powtórzeń będzie zależna od wczytanej liczby boków LBok.
Oto kawałek programu:


Ściany boczne mamy załatwione: łatwizna

Podstawa graniastosłupa
Podstawy są dwie takie same i są to wieloboki foremne, czyli każdy bok ma taką samą szerokość.
Algorytm musi być uniwersalny i mieć możliwość narysowania wieloboku o dowolnej liczbie ścian, podanych przez użytkownika.
Dokładny przepis na wielobok będzie w następnym odcinku, natomiast na razie zrobiłem arkusz kalkulacyjny, który wykreśla wielobok o podanej szerokości ściany oraz zadanej liczbie boków.
Należy do niego wpisać liczbę boków i szerokość ściany. Pozostałe wielkości, promień, kąt zostaną wyjaśnione w następnym odcinku
Zrzut ekranu:


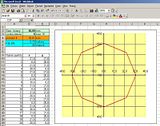
Arkusz można sobie ściągnąć (kliknąć poniższy link, potem "Click here to start download" a następnie "Zapisz") i poeksperymentować, wpisując swoje dane:
http://www.mediafire.com/?552cyt4dx2x

Arkusz ma komórki zabezpieczone przed modyfikacją, ale można to odblokować klikając Narzędzia>Nie chroń arkusza
c.d.n.

[Syzyf]

Hmm, pytań nie ma, oglądalność na poziomie średniej unijnej... Czyli chyba jasno tłumaczę .
Albo zaglądający tutaj, po pierwszym rzucie okiem, zwiewają bez pytań gdzie pieprz rośnie
Zatem w tej ciszy i spokoju kontunuuję dalej.

Ciekawe, że łatwiejsza część programu, rysująca w pętli ściany boczne liczyła 4 wiersze poleceń. Część trudniejsza, rysująca wielobok liczy zaś ... tylko jeden wiersz.

Bardziej mozolna natomiast jest droga prowadząca do tej jednej linijki. Opiszę to dość szczegółowo, ponieważ algorytm ten będzie powtarzał się cały czas (a końca wątku nie widać ). Będzie wykorzystany do rozwijania ostrosłupa, stożka, oraz walców, stożków, graniastosłupów ściętych prosto albo ukośnie. Wszystko opiera się na tej jednej zasadzie.

Przy rysowaniu wieloboku foremnego wykorzystamy 2 fakty:
1. Można go wpisać w okrąg, tzn. każdy wierzchołek leży na jego obwodzie. Do wykreślenia potrzebny będzie promień takiego okręgu.
2. Prowadząc linie od środka okręgu do wierzchołków otrzymuje się trójkąty równoboczne. Trójkątów tych jest tyle ile, boków ma graniastosłup a suma kątów ich wierzchołków wynosi 360 stopni
Można więc łatwo wyznaczyć kąt Beta wierzchołka tych trójkątów oraz znaleźć promień okręgu R:


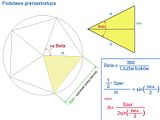
Narysowanie dowolnego wieloboku jest więc proste: obieramy na okręgu jakiś punkt początkowy P1 i obracamy go - niczym wskazówki zegara - o wielokrotności kąta Beta:
Przy pomocy cyrkla i kątomierza można łatwo narysować na kartce dowolny wielobok foremny. Trzeba tylko obliczyć wcześniej promień i kąt wierzchołka trójkąta.


Program jednak nie dysponuje cyrklem i trzeba to przerobić na współrzędne punktów. Jest to chyba łatwiejsze niż znalezienie w moim domu kątomierza, a robi to się tak:


Punkty “ślizgają” się po okręgu i łatwo wyznaczyć ich współrzędne wstawiając do wzorów wielokrotności kąta Beta:


Wiadomo już, jak narysować wielobok o środku w początku układu współrzędnych. Program może jednak operować tylko na współrzędnych dodatnich, trzeba więc przesunąć figurę do I ćwiartki:


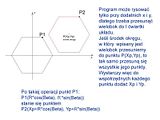
Taki elaborat, żeby wyjaśnić sens jednej linijki programu


Niebawem zmierzę się z ostrosłupem.

[Syzyf]

Witam ponownie - czas na naukę

Ostrosłup foremny

Samo rozwinięcie jest proste co do zasady: ściany boczne są trójkątami stykającymi się bokami, a podstawą jest wielokąt foremny znany z poprzedniego odcinka.
Podstawę więc pominę, skupiając się tylko na bokach:



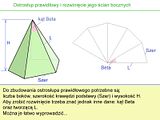
Po wyprowadzeniu:



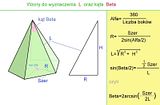
Jeśli ktoś nie pamięta co oznacza arcsin (czytaj: arkus sinus), to jest to funkcja odwrotna do sinusa. Idea tej odwrotności jest prosta jak budowa cepa:
sam sinus mówi jaki jest stosunek boków przy danym kącie.
Arcus zaś zwraca kąt przy danym stosunku boków (Alfa na rysunku poniżej jest kątem "ogólnym", nie z poprzedniego rysunku. Drobna niefortunność):



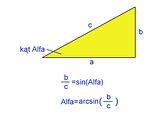
Samo rozwinięcie można zrobić niemal identycznie, jak wyrysowanie wieloboku. Jedyna różnica jest taka, że kąt którym “obracamy” punkt nie dojdzie do wartości 360 stopni:



Pozostało napisać kawałek “programu”:



A w następnym odcinku to, na co wszyscy czekali: ostrosłup ze ściętym płasko czubkiem

[Syzyf]

Ostrosłup ścięty płasko

Zgodnie z obietnicą, dzisiaj będzie ostro: ścinamy gościowi czubek
W życiu chciałoby się nie raz, a tutaj można sobie bezkarnie pohulać.
Choć czubek ścięty, to nadal będzie on bardzo potrzebny. Można powiedzieć, że aby rozwinąć ostrosłup ścięty, trzeba mu czubek założyć z powrotem:





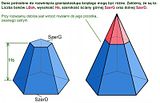
O rozwijaniu podstawy i powierzchni górnej nie ma co pisać, bo wiadomo co i jak z poprzednich odcinków.
Algorytm ten zawiera w sobie w pewnym sensie poprzedni. Jeśli przyjmie się szerokość ściany górnej równą 0, to powstanie rozwinięcie zwykłego ostrosłupa ze szpicem.

Następny odcinek co najmniej za tydzień, ale będę myślał nad kolejnym tematem.
Jeśli kogoś interesuje “jak to się robi?”, czyli opis jakiegoś konkretnego rozwinięcia – niech napisze.
Nie obiecuję, że będę w stanie to zrobić, bo głowa już nie ta, ale pomyśleć zawsze można
No i jest pomocna ręka Forum...